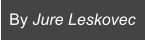Higher-order organization of complex networks
Many networks are known to exhibit rich, lower-order connectivity patterns that can be captured at the level of individual nodes and edges. In this project, we focus on finding higher-order organization of complex networks at the level of small network subgraphs (motifs). To this end, we cluster the nodes of a graph based on motifs instead of edges.
Higher-order Organization of Complex Networks.
Austin R. Benson, David F. Gleich, and Jure Leskovec.
Science, vol. 353, no. 6295, pp. 163-166, 2016.
[Paper] [Supplementary Materials]
Motif-based spectral clustering method
Our goal is to find sets of nodes with small motif conductance. The
motif conductances of a set S of nodes with respect to a motif M is
φM(S) = cutM(S, S) / min(volM(S),
volM(S)), where
cutM(S, S) is the
number of instances of motif M with at least one node in S and one in
S,
and volM(S) is the number of nodes in instances of M that reside in S.
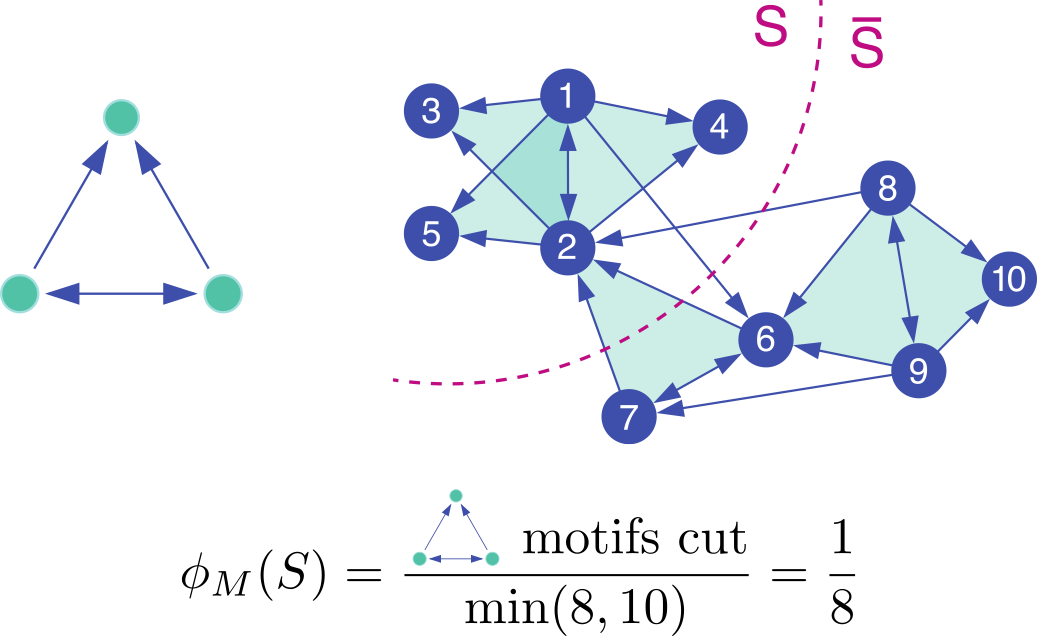
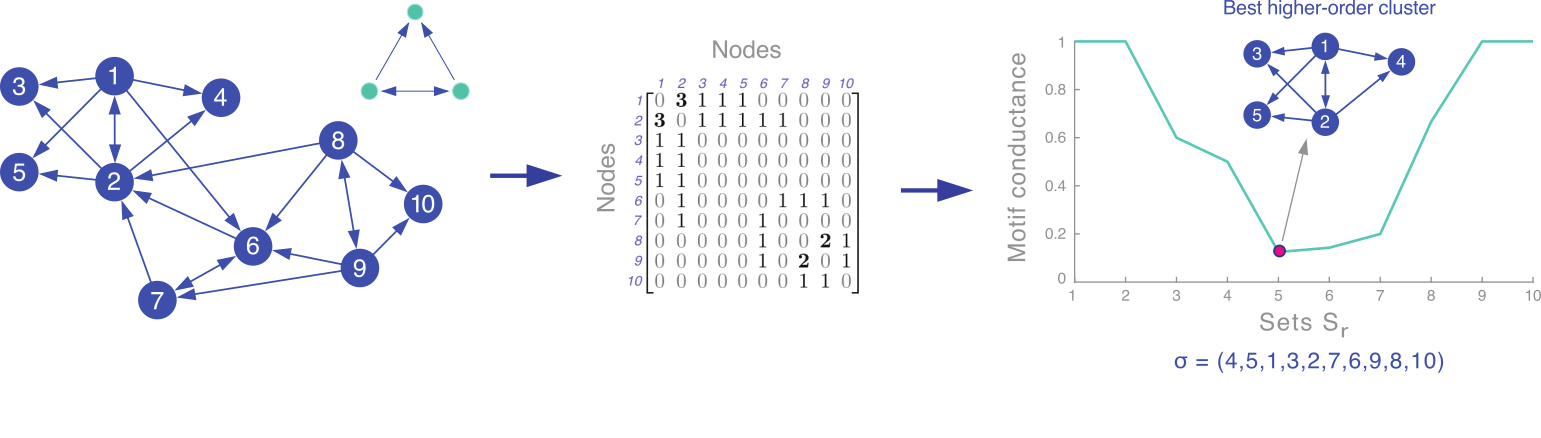
Our spectral clustering technique for finding sets S with small motif conductance is:
- Given a network and a motif M of interest, form the motif adjacency matrix whose (i, j) entries are the number of times that nodes i and j co-occur in instances of M.
- Compute the spectral ordering σ of the nodes from the normalized Laplacian of the motif adjacency matrix.
- Find the prefix set S of σ with the smallest motif conductance; formally: S = argmin φM(Sr), where Sr = {σ1, ..., σr}.
Examples
In many cases, we know that particular motifs are important for a given network. For example, the bifan motif is known to occurr frequently in neuronal networks. We can use this motif to find clusters in networks such as C. elegans, pictured here.
Often, the structure of the motif shows up in the cluster found by the algorithm. This contrasts with traditional edge-based clusters, which are typically densely connected. Here is one example from the Twitter follower network.

Our framework is general enough to handle signed, weighted, and colored motifs. Below is an example of motif-based clustering for the so-called coherent feedforward loop motifs in the S. cerevisiae transcriptional regulation network.

Sometimes, we may not know which motif is of interest. We can run motif-based clustering for several motifs and see which motifs give good results. In the following example, looking at motif conductance suggests that M6 organizes the network. The extracted clusters are clearly shaped around motif M6.

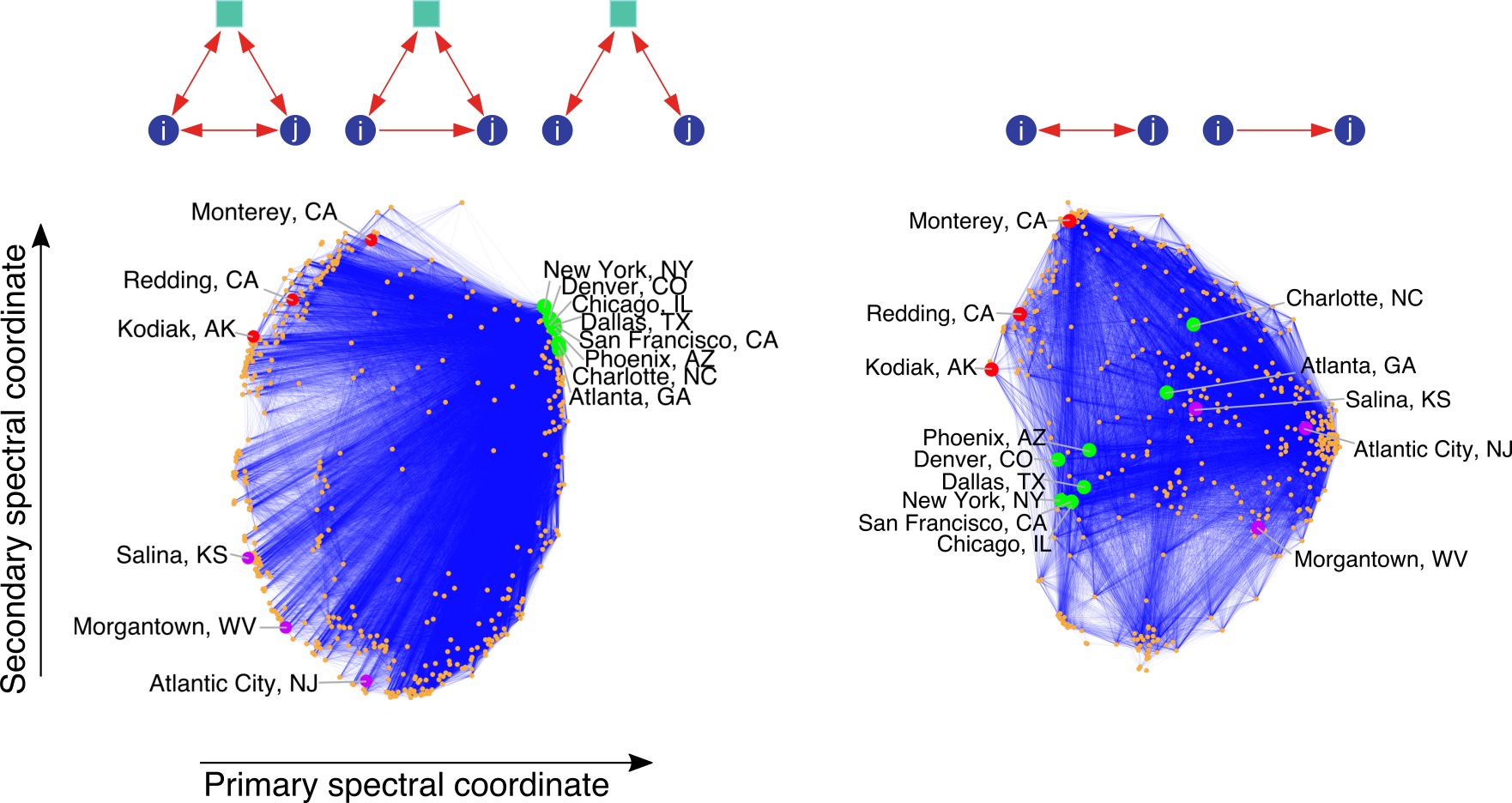
Finally, in some cases, we seek richer structure from our data that cannot be realized just by clusters of nodes. In the following example, we use a spectral embeddings from the motif adjacency matrix to capture higher-order structure in a transportation reachability network.