MAPPR for local higher-order clustering
MAPPR (Motif-based Approximate Personalized PageRank) is an algorithmic framework for local higher-order clustering. Given any graph, a motif of interest, and a target node, it can find a local cluster around this node with minimal motif conductance.
Motivation
Local graph clustering methods are attractive because they enable targeted clustering around a given seed node and are faster than traditional global graph clustering methods because their runtime does not depend on the size of the input graph. However, current local graph partitioning methods are not designed to account for the higher-order structures crucial to the network, nor can they effectively handle directed networks. In this project, we introduce a new class of local graph clustering methods that address these issues by incorporating higher-order network information captured by small subgraphs, also called network motifs. We develop the Motif-based Approximate Personalized PageRank (MAPPR) algorithm that finds clusters containing a seed node with minimal motif conductance. We also generalize existing theory to prove the fast running time (independent of the size of the graph) and obtain theoretical guarantees on the cluster quality.
Local Higher-Order Graph Clustering.
Hao Yin, Austin R. Benson, Jure Leskovec, and David F. Gleich.
To appear in KDD, 2017.
Method
Our goal is to find a subset of nodes around the seed node with small motif conductance. The
motif conductances of a set S of nodes with respect to a motif M is
φM(S) = cutM(S, S) / min(volM(S),
volM(S)), where
cutM(S, S) is the
number of instances of motif M with at least one node in S and one in
S,
and volM(S) is the number of nodes in instances of M that reside in S.
Our MAPPR method for finding sets S with small motif conductance is:
- Given a network and a motif M of interest, form the motif adjacency matrix whose (i, j) entries are the number of times that nodes i and j co-occur in instances of M.
- Compute ordering on nodes based on the approximated Personalized PageRank vector seeded at the target node.
- Find the prefix set S of σ with the smallest motif conductance; formally: S = argmin φM(Sr), where Sr = {σ1, ..., σr}.
Examples
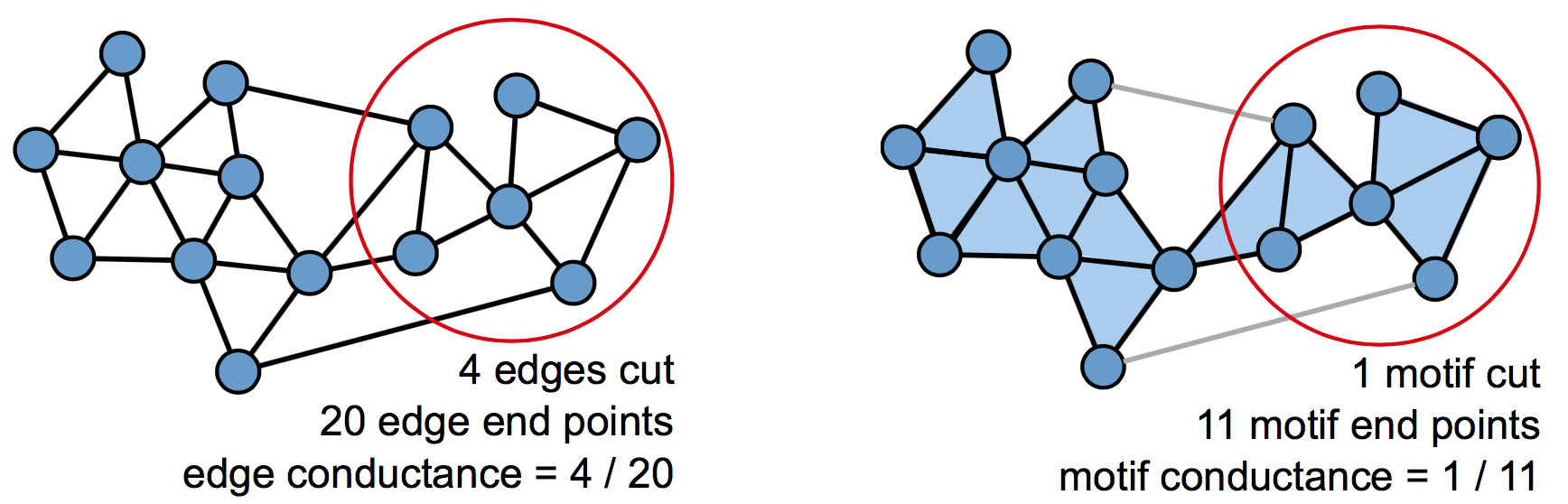
We compare the ground truth community recovery performance of our MAPPR method with motif being triangle, with the regular APPR method which is equivalent to our MAPPR method with motif being edge. We use two random graph models with planted ground truth communities: the planted partition model and the LFR model. We compute the F1 score of the two methods with different mixing parameters (fraction of edges cross communities) in the graph generation process while fixing all other parameters. Experiment results show that there is a huge region in parameter spaces where MAPPR method significantly outperforms the regular APPR method.
We also compare the recovery performance of the two methods on real-world networks with ground truth communities. Although these graphs have as many as 1.8 billion edges, the MAPPR method takes at most a few seconds per seed once the graph is in memory. Details of these experiments are explained in the paper.