Hyperbolic Graph Convolutional Neural Networks

• Motivation
• Method
• Code
• Datasets
• Contributors
• References

Motivation

Graph convolutional neural networks (GCNs) map nodes in a graph to Euclidean embeddings, which have been shown to incur a large distortion when embedding real-world graphs with scale-free or hierarchical structure.

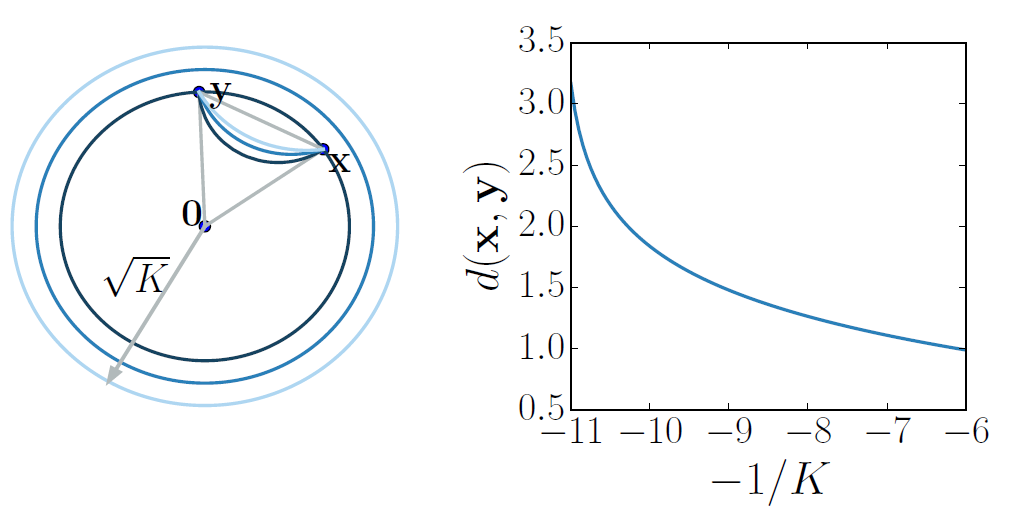
Hyperbolic geometry offers an exciting alternative, as it enables embeddings with much smaller distortion. In particular, if volume in graphs is defined as the number of nodes within some distance to a center node, it grows exponentially with respect to that distance for regular trees. However, the volume of balls in Euclidean space only growspolynomially with respect to the radius, leading to high distortion tree embeddings, while in hyperbolic space, this volume grows exponentially. The curvature (-1/K) of the hyperbolic space also plays a key role. As the curvature becomes more negative, the distance between the points with the same coordinates increases. Thus is more suitable for hierarchical graphs with large degree / fanout.

Method

We propose HGCN with the following components:

• We derive the core transformation of GCNs in the hyperboloid modelof hyperbolic space to transform the input features which lie in Euclidean space into hyperbolic embeddings.
• We introduce a hyperbolic attention-based aggregation scheme that captures nodehierarchies.
• We apply feature transformations in hyperbolic spaces of different trainable curvaturesat different layers to learn hyperbolic embeddings that preserve the graph structure and a notion ofhierarchy for nodes in the graph.

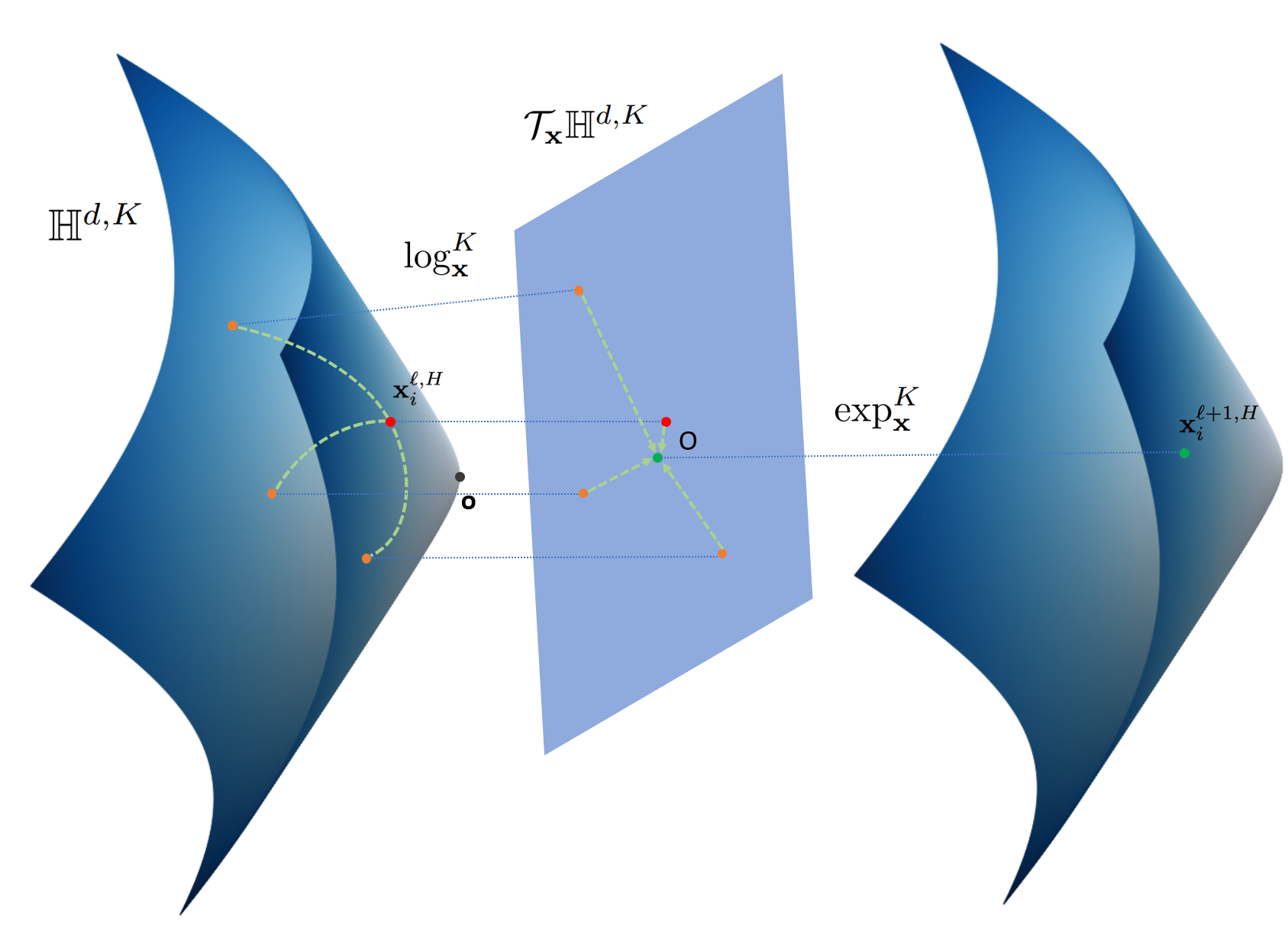
The concept of tangent space is important when performing neural network operation in hyperbolic spaces. The exponential map maps points in the tangent space of another reference point to the hyperbolic space. The logarithmic map is the inverse operation that maps the points back to the tangent space.

HGCN performs the mapping of input features to the hyperboloid manifold via the exponential map, and use exp/log map and parallel transport for the linear transformation used in graph convolution. Aggregation is also a crucial step in GCNs as it captures neighborhood structures and features with message passing. We use attention-based aggregation with the following expression:

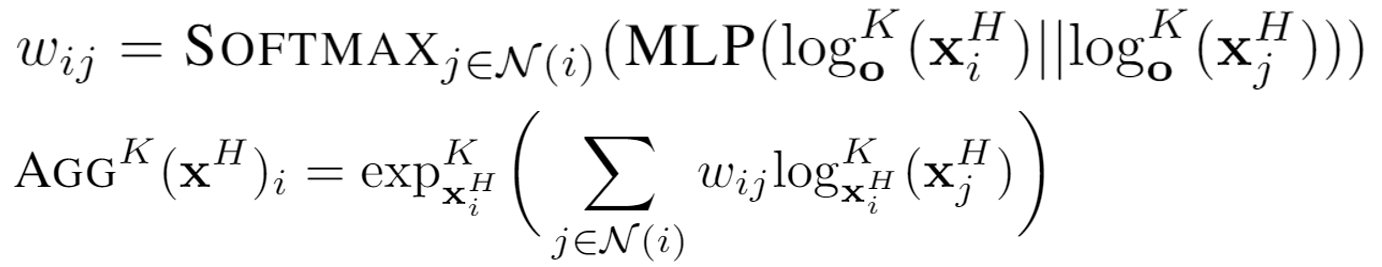
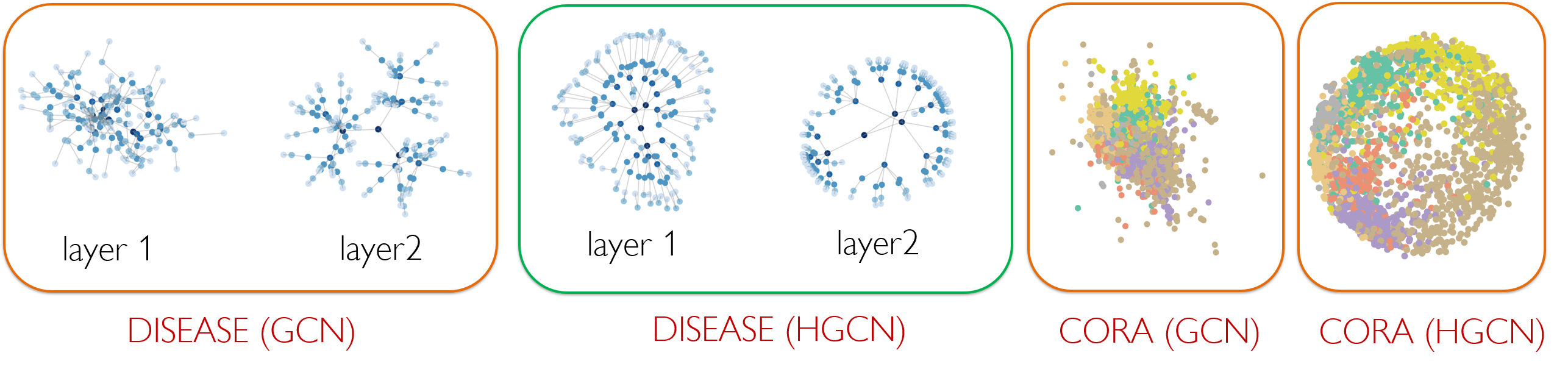
Finally we perform non-linear activation and transformation of the embedding to next layer embeddings, which are in a hyperbolic space with a different curvature. We comprehensively evaluate our experiments on a variety of networks, on both node classification and link prediction tasks, in transductive and inductive settings. In the following, we show the first layer and second layer embedding of the disease tree dataset for both GCN and HGCN (in 2 dimensions). HGCN can map the nodes to embeddings of different hyperbolic space with different curvature at each layer, resulting in low distortion embedding for hierarchical data. We also show the comparison of embedding for CORA dataset in low dimensions, showing that hyperbolic embeddings are more superior compared to Euclidean GCN embeddings when embeddings have low dimensions.

Please refer to our paper for detailed explanations and more results.

Code

A reference implementation of HGCN in Python is available on GitHub.

Datasets

The datasets used by HGCN are included in the code repository.

Contributors

The following people contributed to HGCN:
Ines Chami*
Rex Ying*
Christopher Ré
Jure Leskovec

References

Hyperbolic Graph Convolutional Neural Networks. I. Chami, R. Ying, C. Ré, J. Leskovec. Neural Information Processing Systems (NeurIPS), 2019.