Inductive Representation Learning in Temporal Networks via Causal Anonymous Walks
We introduce Causal Anonymous Walks (CAW) for inductive representation learning in temporal networks. CAWs are extracted by temporal random walks and work as automatic retrieval of temporal network motifs to represent network dynamics, while avoiding the time-consuming selection and counting of those motifs. CAWs adopt a novel anonymization strategy that replaces node identities with the hitting counts of the nodes based on a set of sampled walks to keep the method inductive, and simultaneously establish the correlation between motifs. The neural architectures derived out of CAWs, CAW-N-Mean, CAW-N-Attn, are the current SOTA on both transductive and inductive link prediction tasks in temporal networks.
Motivation
Temporal networks serve as abstractions of many real-world dynamic systems. These networks typically evolve according to certain laws, such as the law of triadic closure, feed-forward control loops, etc. Inductive representation learning of temporal networks should be able to capture such laws and further be applied to systems that follow the same laws but have not been unseen during the training stage. These laws may only depend on structures such as the triadic closure or feed-forward control. These laws may also correlate with node attributes, such as interactions between people affected by their gender and age. But in both cases, the laws should be independent from network node identities. Although previous works tend to learn inductive models by removing node identities, they essentially fail to be truly inductive.
Our idea for inductive learning is inspired by the recent investigation on temporal network motifs that correspond to connected subgraphs with links that appear within a restricted time range. Temporal network motifs essentially reflect network dynamics: Both triadic closure and feed-forward control can be viewed as temporal network motifs evolving (Fig. 1); An inductive model should predict the 3rd link in both cases when it captures the correlation of these two links as they share a common node, while the model is agnostic to the node identities of these motifs.

Method
Our CAW model has two important properties (Fig. 2): (1) Causality extraction—a CAW starts from a link of interest and backtracks several adjacent links over time to encode the underlying causality of network dynamics. Each walk essentially gives a temporal network motif; (2) Set-based anonymization—CAWs remove the node identities over the walks to guarantee inductive learning while encoding relative node identities based on the counts that they appear at a certain position according to a set of sampled walks. Relative node identities guarantee that the structures of motifs and their correlations are still kept after removing node identities. To predict temporal links between two nodes of interest, we propose a model CAW-Network (CAW-N) that samples a few CAWs related to the two nodes of interest, encodes and aggregates these CAWs via RNNs and set-pooling respectively to make the prediction.
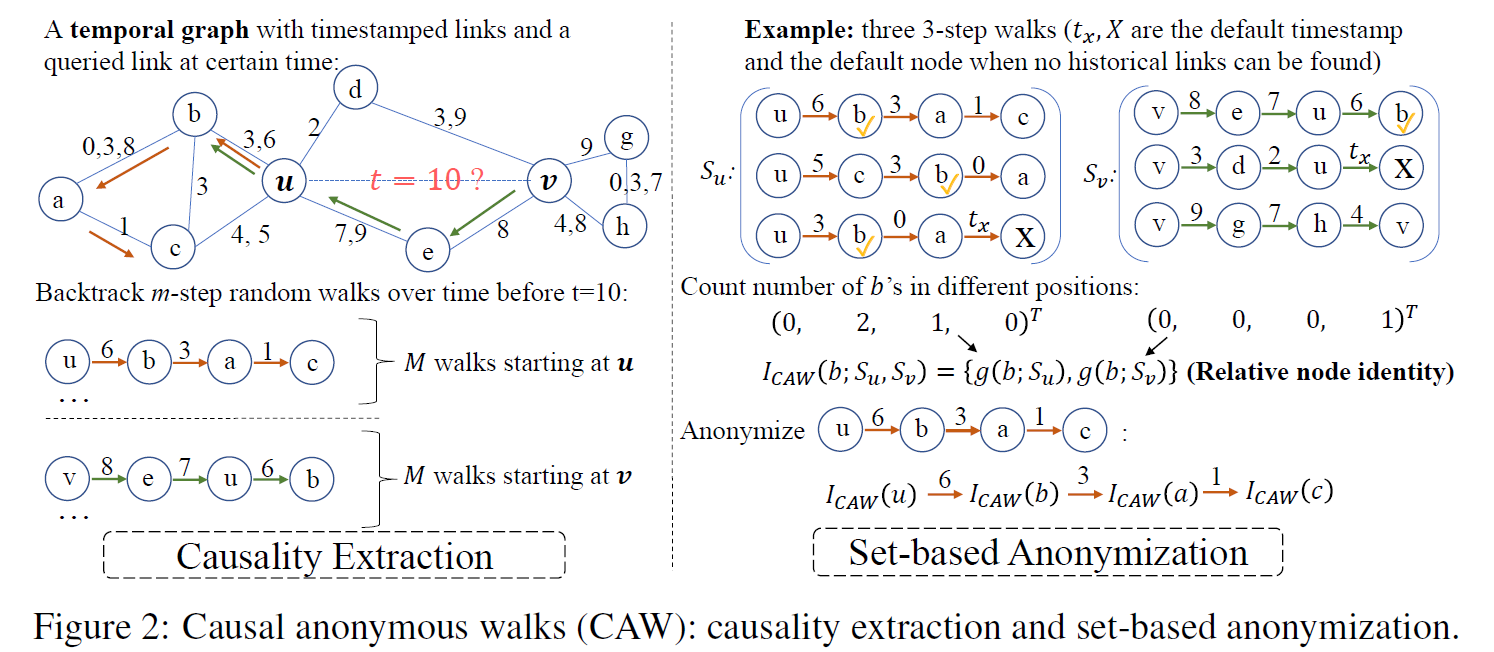
CAW-N significantly decreases the feature-engineering effort in traditional motif selection and counting approaches and keeps fine-grained temporal information. In addition, CAW-N is also paired with a CAW sampling method with constant memory and time cost, which conduces to online learning.
Experiment
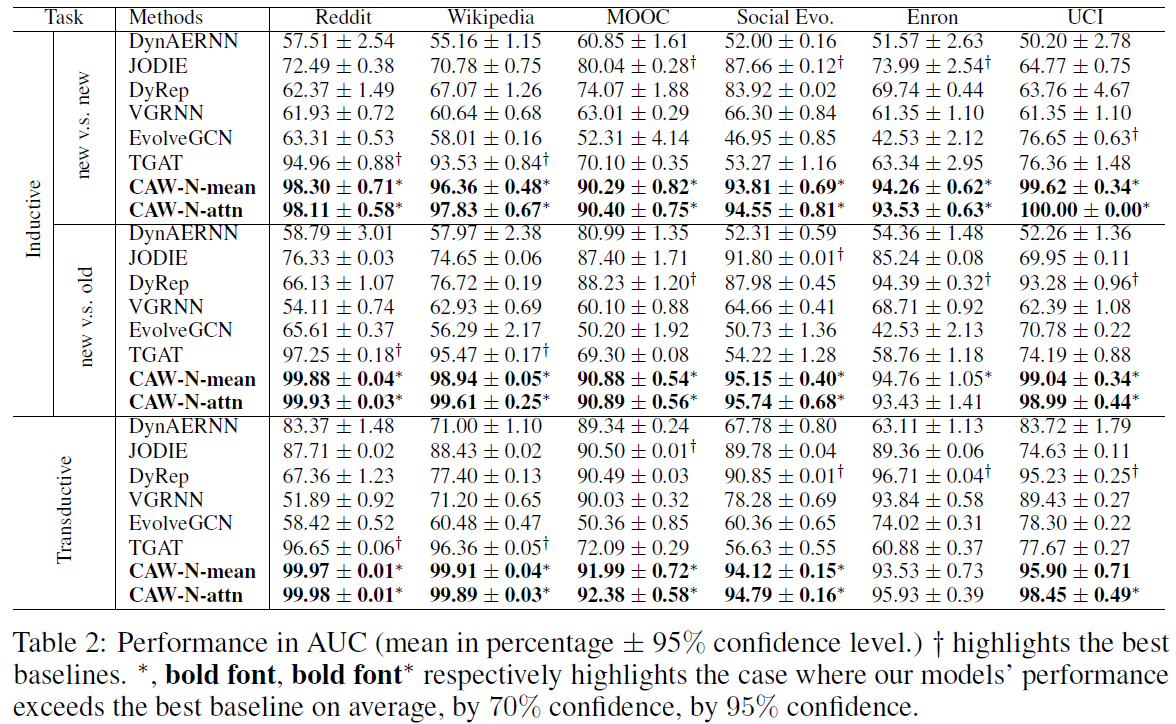
Experiments show that CAW-N is extremely effective (Fig. 3). The two variants of CAW-N that we propose are evaluated to predict links over 6 real-world temporal networks. CAW-N outperforms all SOTA methods by about 15% averaged over 6 networks in the inductive setting and also significantly beat all SOTA methods over 5 networks in the transductive setting;
Code & Datasets
A reference PyTorch implementation of the two variants of CAW-N, CAW-N-Mean and CAW-N-Attn, is available on GitHub. Links to the datasets used by CAW-N are given in the code repository.Paper
The preprint is available here (to appear in ICLR'21).Contributors
The following people contributed to the paper:
Yanbang Wang
Yen-Yu Chang
Yunyu Liu
Jure Leskovec
Pan Li
References
Inductive Representation Learning in Temporal Networks via Causal Anonymous Walks. Yanbang Wang, Yen-Yu Chang, Yunyu Liu, Jure Leskovec, Pan Li. International Conference on Learning Representations (ICLR), 2021.