Design Space for Graph Neural Networks

• Motivation
• Method
• Key Results
• Code and Datasets
• Contributors
• References

Motivation

Graph Neural Networks (GNNs) have evolved immensely, with growing number of new architectures and applications being proposed. However, the current literature focuses on proposing and evaluating specific designs of GNNs such as GCN or GAT, as opposed to studying the design space of GNNs that consists of a Cartesian product of design dimensions such as the number of layers or the type of aggregation function.
Additionally, these GNN designs are currently evaluated on a limited variety of tasks where the best designs can be drastically different, yet few efforts have been made to understand how the best GNN designs can transfer across tasks.

Method

To tackle the above-mentioned issues, we highlight three central components in our study, namely GNN design space, GNN task space, and design space evaluation.

• A general GNN design space is used to cover important design aspects that researchers will encounter during algorithm development.
• A GNN task space with quantitative similarity metric is built, so that novel tasks can be identified and similar tasks can share the best performing GNN designs.
• An efficient and effective design space evaluation allows insights to be distilled from a huge number of model-task combinations.
• Finally, we develop GraphGym, a convenient code platform that supports instantiating these components.

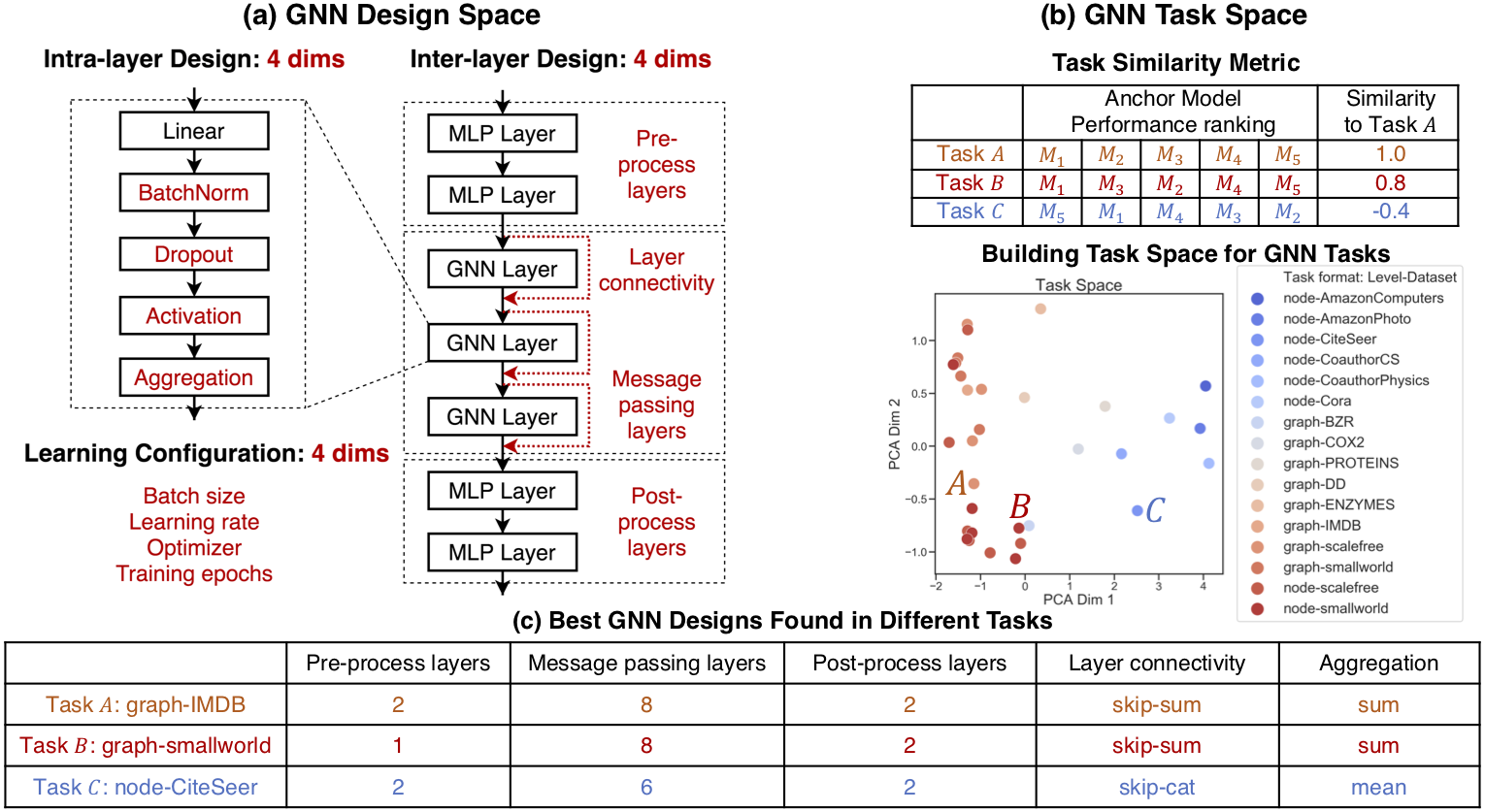
GNN design space. We define a general design space of GNNs over intra-layer design, inter-layer design and learning configuration, as is shown in Figure 1(a). The design space consists of 12 design dimensions, resulting in 315K possible designs. We aim to cover many rather than all possible design dimensions in the design space. Our purpose is not to propose the best possible GNN design space, but to demonstrate how focusing on the design space rather than individual designs can enhance GNN research.

GNN task space. We propose a quantitative task similarity metric to characterize different tasks, as is shown in Figure 1(b). Specifically, the similarity between 2 tasks is computed by applying a fix set of GNNs to 2 tasks then measuring the Kendall rank correlation [1] of the performance of these GNNs. We consider 32 tasks consists of (1) synthetic tasks including 12 node classification tasks and 8 graph classification tasks, (2) real-world tasks including 6 node classification and 6 graph classification tasks.

Design space evaluation. Our goal is to gain insights from the defined GNN design space, such as “Is Batch Normalization generally useful for GNNs?”. However, the defined design space and task space leads to over 10M possible combinations, prohibiting a full grid search. We design a controlled random search evaluation to efficiently understand the trade-offs of each design dimension, illustrated in Figure 2.

Key Results

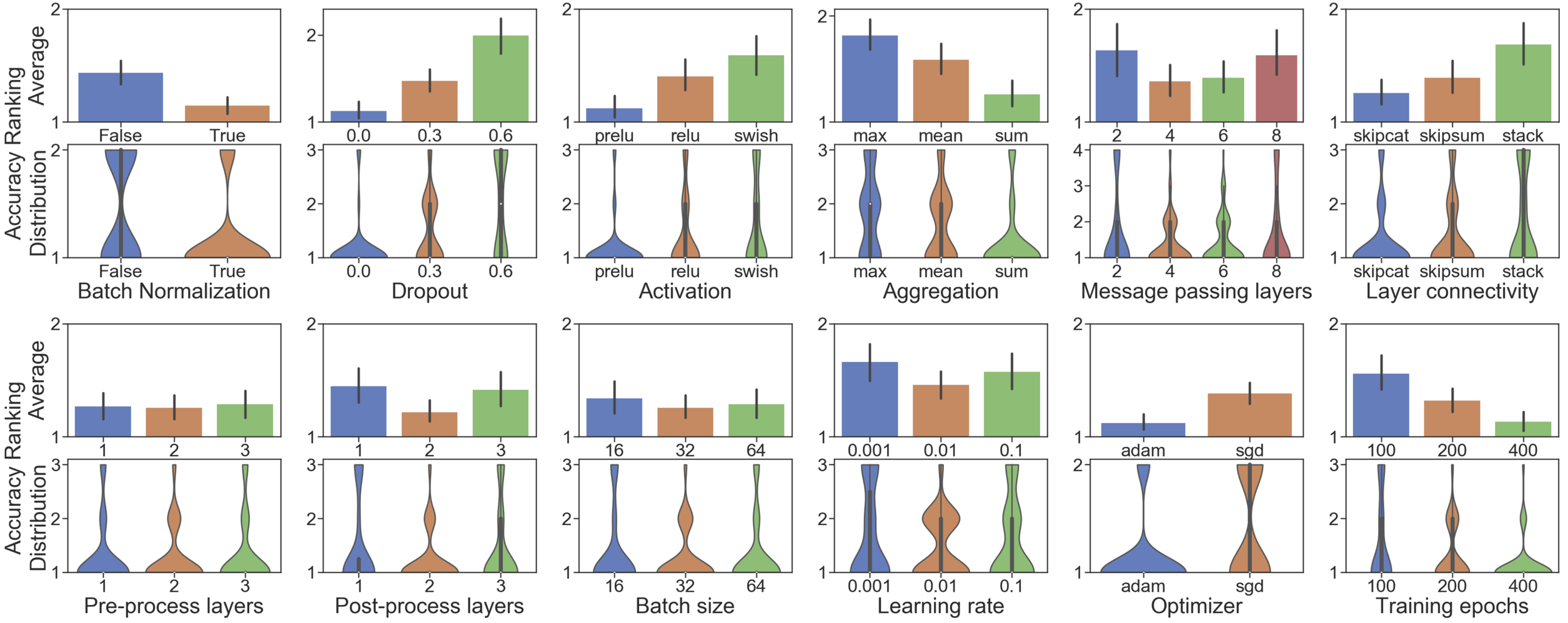
GNN Design Space Evaluation. Firstly, we apply the proposed evaluation technique to each of the 12 design dimensions of the proposed design space. The results are shown in Figure 3. Overall, the proposed evaluation framework provides a solid tool to rigorously verify new GNN design dimensions. By conducting controlled random search over 10M possible model-task combinations (96 experiments per design dimension), our approach provides a more convincing guideline on GNN designs, compared with the common practice that only evaluate a new design dimension on a fixed GNN design (e.g., 5-layer, 64-dim, etc.) on a few graph prediction tasks (e.g., Cora or ENZYMES).

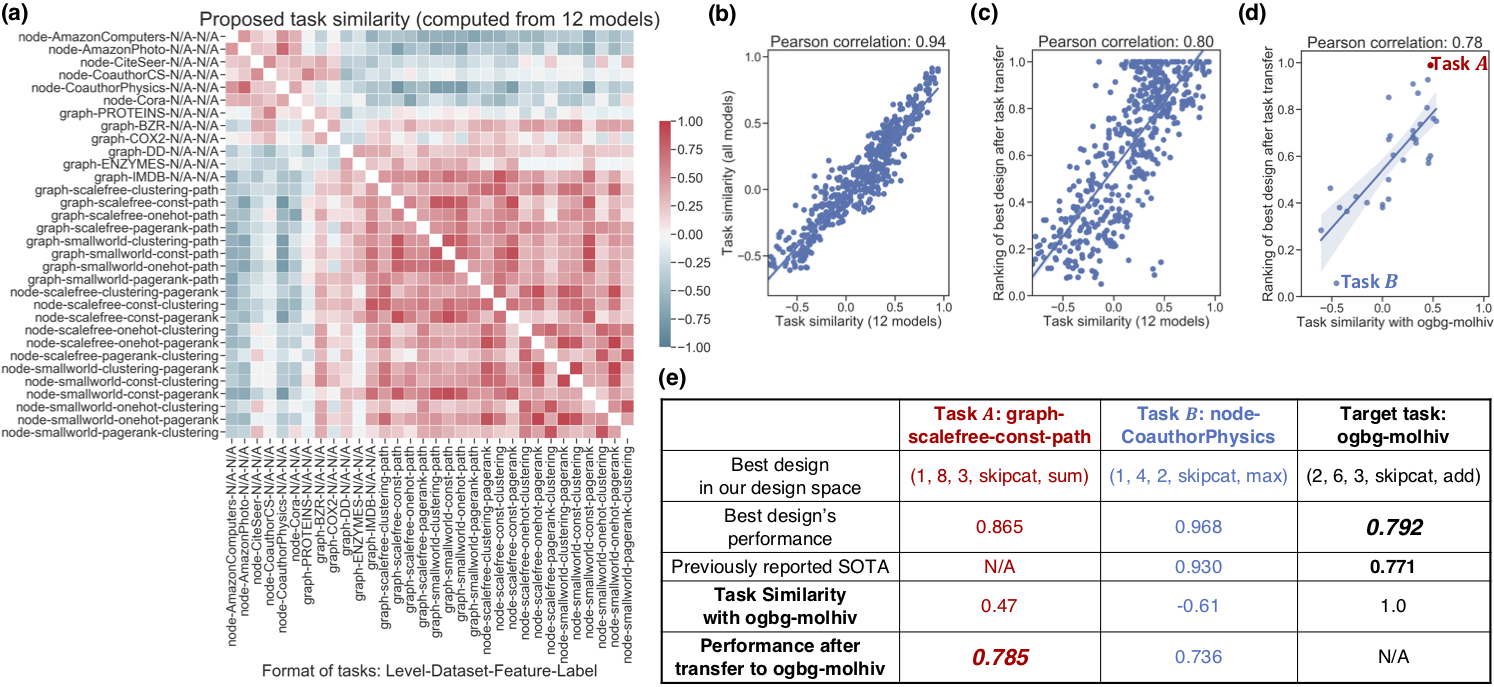
Efficacy of GNN Task Space. We build a task space via the proposed task similarity metric. Figure 4(a) visualizes the task similarities computed using the proposed metric. The key finding is that tasks can be roughly clustered into two groups: (1) node classification over real-world graphs, (2) node classification over synthetic graphs and all graph classification tasks.
Additionally, we show in Figure 4(e) that the proposed task similarity can guide transferring top designs to a novel learning task, ogbg-molhiv, without grid search.

Please refer to our paper for detailed explanations and more results.

Code and Datasets

We release GraphGym on GitHub. The datasets are included in the code repository.

Contributors

Jiaxuan You
Rex Ying
Jure Leskovec

References

Design Space for Graph Neural Networks. Jiaxuan You, Rex Ying, Jure Leskovec. Neural Information Processing Systems (NeurIPS), 2020.