Distance Encoding: Design Provably More Powerful Neural Networks for Graph Representation Learning
Distance Encoding is a general class of graph-structure-related features that can be utilized by graph neural networks to improve the structural representation power. Given a node set whose structural representation is to be learnt, DE for a node over the graph is defined as a mapping of a set of landing probabilities of random walks from each node of the node set of interest to this node. Distance encoding generally includes measures such as shortest-path-distances and generalized PageRank scores. Distance encoding can be merged into the design of graph neural networks in simple but effective ways: First, we propose DEGNN that utilizes distance encoding as extra node features. We further enhance DEGNN by allowing distance encoding to control the aggregation procedure of traditional GNNs, which yields another model DEAGNN. Since distance encoding purely depends on the graph structure and is independent from node identifiers, it has inductive and generalization ability.
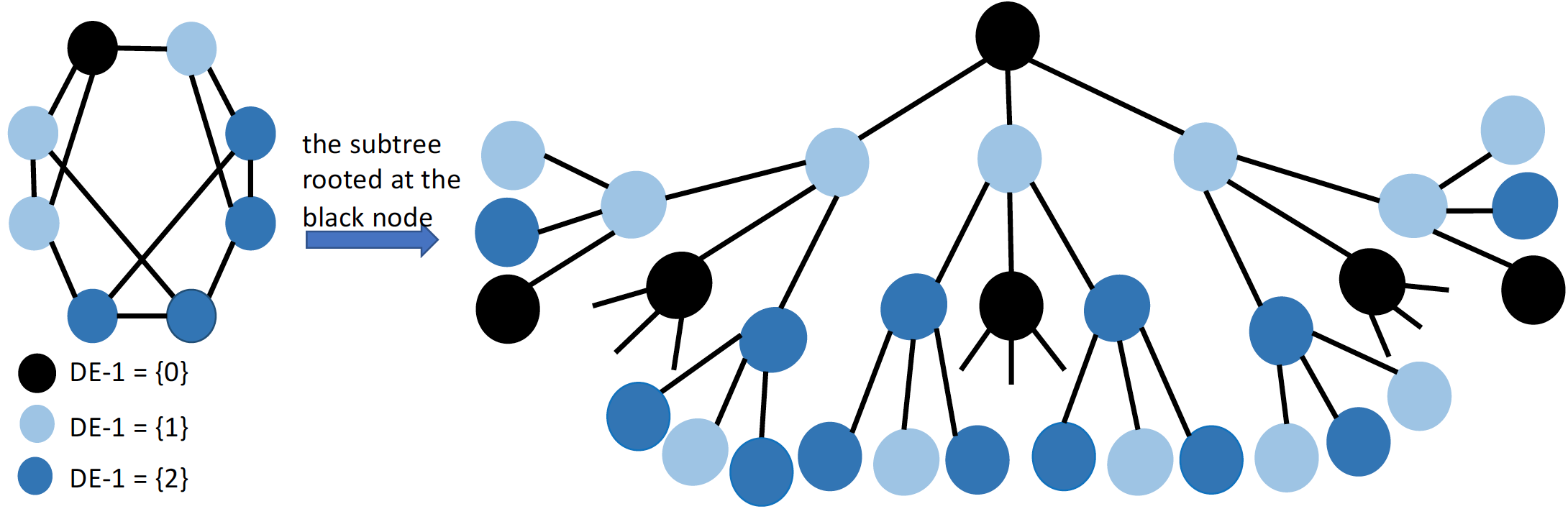
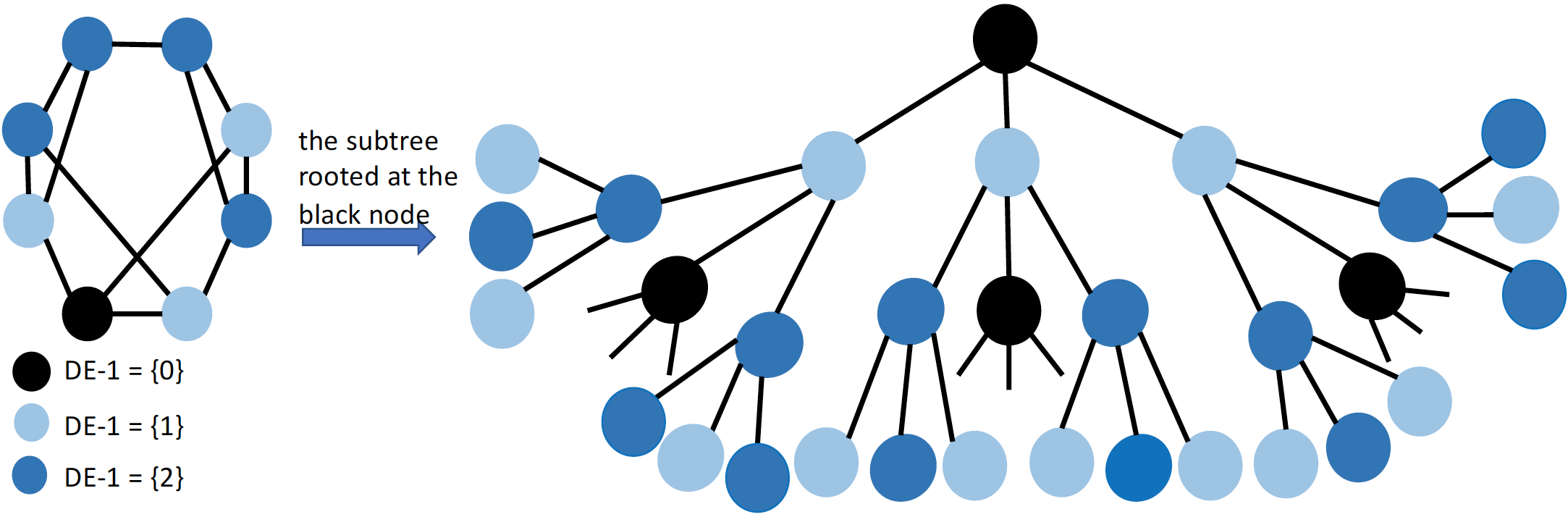
The power for structural representation learning based on distance encoding can be rigorously characterized. Specifically, we may prove that both DEGNN and DEAGNN are able to distinguish two non-isomorphic equal-sized node sets (including nodes, node-pairs, ..., entire-graphs) that are embedded in almost all regular graphs where traditional GNNs always fail if no discriminatory node/edge attributes are available. We also prove that these two models are not more powerful than traditional GNNs without discriminatory node/edge attributes to learn the structural representations of nodes over distance regular graphs, which implies the limitation of distance encoding. However, we may show that both models have extra power to learn the structural representations of node-pairs over distance regular graphs. Both DEGNN and DEAGNN are evaluated on three levels of tasks including roles of node-role classification (node-level), link prediction (node-pair-level), triangle prediction (node-triad-level). Note that triangle prediction is to predict higher-order network motifs that are known to be challenging and very few works have been proposed before for this task. Both models significantly outperform traditional GNNs on all three tasks by up-to 15% improvement in prediction average accuracy. Both methods also outperform other state-of-the-art baselines specifically designed for these tasks.Motivation
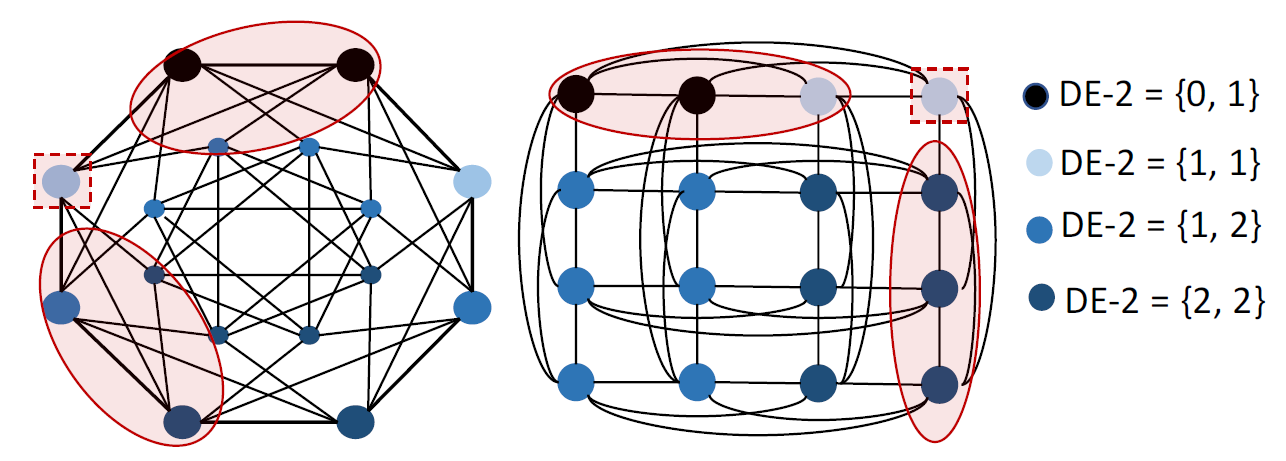
Structural representation learning of a node set has many applications such as node-role prediction based on a single node representation, link prediction based on node-pair representation, molecule prediction based on entire-graph representation. Graph neural networks (GNNs), have recently become almost the default choice to learn structural representations. Despite their great success, recent works proved that the structural representation power of most GNNs, such as GCN, GAT, GraphSAGE, GIN, MPNN and many well-known GNNs, is bounded by 1-Weisfeiler-Lehman test (Weisfeiler & Lehman, 1968). We refer these GNNs as WLGNN. The figure below shows a case for this. The graph is a 3-regular graph with 8 nodes and no attributes. The nodes with same colors are structurally equivalent because of the horizontal reflexivity and the node permutation shown in the right subfigure. The nodes with different colors are not structurally equivalent. However, WLGNN will assign all nodes with same representations. Furthermore, WLGNN cannot distinguish all the node-pairs highlighted by the dashed circles no matter whether these node-pairs correspond to edges or not.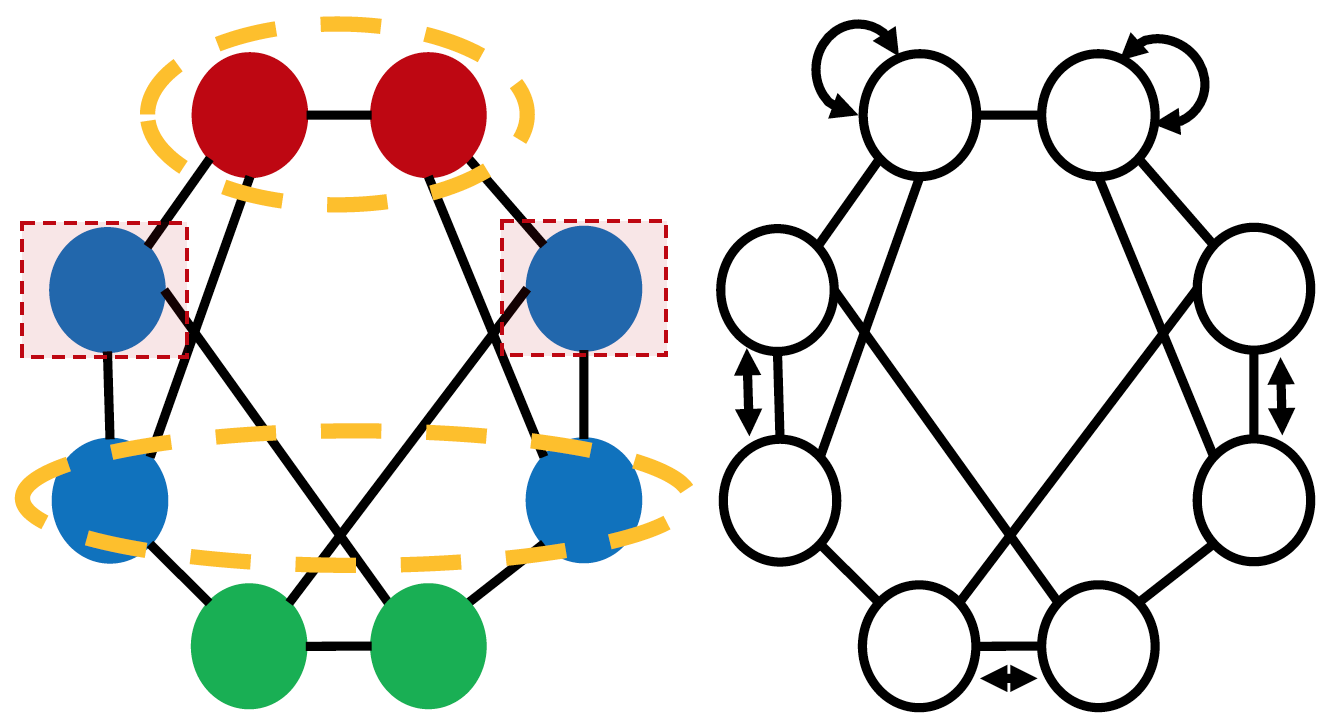
Code
A reference implementation of DEGNN and DEAGNN in Python is available on GitHub.Datasets
The datasets used by Distance Encoding project are included in the code repository.Contributors
The following people contributed to Distance Encoding project:Pan Li
Yanbang Wang
Hongwei Wang
Jure Leskovec