Graph Convolutional Prediction of Protein Interactions in Yeast¶
(This demo is a part of Deep Learning for Network Biology tutorial.)
In this example, we demonstrate the utility of deep learning methods for an important prediction problem on biological graphs. In particular, we consider the problem of predicting protein-protein interactions (PPIs).
Protein-protein interactions (PPIs) are essential to almost every process in a cell. Understanding PPIs is crucial for understanding cell physiology in normal and disease states. Furthermore, knowledge of PPIs can be used:
- for drug development, since drugs can affect PPIs,
- to assign roles (i.e., protein functions) to uncharacterized proteins,
- to characterize the relationships between proteins that form multi-molecular complexes, such as the proteasome.
We represent the totality of PPIs that happen in a cell, an organism or a specific biological context with a protein-protein interaction network. These networks are mathematical representations of all physical contacts between proteins in the cell.
The development of large-scale PPI screening techniques, especially high-throughput affinity purification combined with mass-spectrometry and the yeast two-hybrid assay, has caused an explosion in the amount of PPI data and the construction of ever more complex and complete interaction networks. For example, the figure below is a graphical representation of three different types of protein-protein interaction networks in yeast S. cerevisiae. The structure of the binary interaction network is obviously different from the structure of the co-complex interaction network. The network structure of the literature-curated dataset resembles that of the co-complex dataset, even though the literature-curated datasets are reported to contain mostly binary interactions.
However, current knowledge of protein-protein interaction networks is both incomplete and noisy, as PPI screening techniques are limited in how many true interactions they can detect. Furthermore, PPI screening techniques often have high false positive and negative rates. These limitations present a great opportunity for computational methods to predict protein-protein interactions.
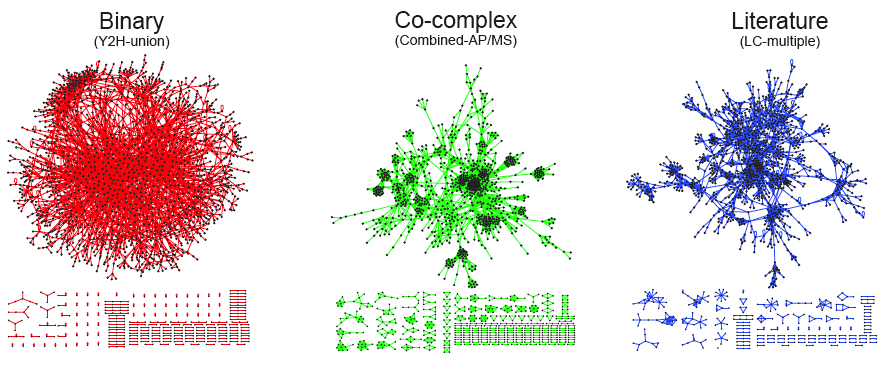
Image taken from: http://interactome.dfci.harvard.edu/S_cerevisiae
In this demo, we take the yeast protein-protein interaction network (download the preprocessed network) and use the network to build a model for predicting new protein-protein interactions. We formulate this prediction task as a link prediction problem on unweighted and undirected networks and use a graph convolutional neural network to solve the task.
Note that link prediction is a standard prediction task in network biology, and thus this example can be easily extended and adapted to many other biomedical applications.
Graph Convolutional Neural Network (GCN)¶
In what follows, we give a complete Tensorflow implementation of a two-layer graph convolutional neural network (GCN) for link prediction. We closely follow the GCN formulation as presented in Kipf et al., ICLR 2017.
from __future__ import division
from __future__ import print_function
import time
import numpy as np
import scipy.sparse as sp
import networkx as nx
import tensorflow as tf
from sklearn.metrics import roc_auc_score
from sklearn.metrics import average_precision_score
# Set random seed
seed = 123
np.random.seed(seed)
tf.set_random_seed(seed)
# Settings
flags = tf.app.flags
FLAGS = flags.FLAGS
flags.DEFINE_float('learning_rate', 0.01, 'Initial learning rate.')
flags.DEFINE_integer('epochs', 20, 'Number of epochs to train.')
flags.DEFINE_integer('hidden1', 32, 'Number of units in hidden layer 1.')
flags.DEFINE_integer('hidden2', 16, 'Number of units in hidden layer 2.')
flags.DEFINE_float('dropout', 0.1, 'Dropout rate (1 - keep probability).')
Various Utility Functions¶
def load_data():
g = nx.read_edgelist('yeast.edgelist')
adj = nx.adjacency_matrix(g)
return adj
def weight_variable_glorot(input_dim, output_dim, name=""):
init_range = np.sqrt(6.0 / (input_dim + output_dim))
initial = tf.random_uniform(
[input_dim, output_dim], minval=-init_range,
maxval=init_range, dtype=tf.float32)
return tf.Variable(initial, name=name)
def dropout_sparse(x, keep_prob, num_nonzero_elems):
noise_shape = [num_nonzero_elems]
random_tensor = keep_prob
random_tensor += tf.random_uniform(noise_shape)
dropout_mask = tf.cast(tf.floor(random_tensor), dtype=tf.bool)
pre_out = tf.sparse_retain(x, dropout_mask)
return pre_out * (1. / keep_prob)
def sparse_to_tuple(sparse_mx):
if not sp.isspmatrix_coo(sparse_mx):
sparse_mx = sparse_mx.tocoo()
coords = np.vstack((sparse_mx.row, sparse_mx.col)).transpose()
values = sparse_mx.data
shape = sparse_mx.shape
return coords, values, shape
def preprocess_graph(adj):
adj = sp.coo_matrix(adj)
adj_ = adj + sp.eye(adj.shape[0])
rowsum = np.array(adj_.sum(1))
degree_mat_inv_sqrt = sp.diags(np.power(rowsum, -0.5).flatten())
adj_normalized = adj_.dot(degree_mat_inv_sqrt).transpose().dot(degree_mat_inv_sqrt).tocoo()
return sparse_to_tuple(adj_normalized)
def construct_feed_dict(adj_normalized, adj, features, placeholders):
feed_dict = dict()
feed_dict.update({placeholders['features']: features})
feed_dict.update({placeholders['adj']: adj_normalized})
feed_dict.update({placeholders['adj_orig']: adj})
return feed_dict
def mask_test_edges(adj):
# Function to build test set with 2% positive links
# Remove diagonal elements
adj = adj - sp.dia_matrix((adj.diagonal()[np.newaxis, :], [0]), shape=adj.shape)
adj.eliminate_zeros()
adj_triu = sp.triu(adj)
adj_tuple = sparse_to_tuple(adj_triu)
edges = adj_tuple[0]
edges_all = sparse_to_tuple(adj)[0]
num_test = int(np.floor(edges.shape[0] / 50.))
num_val = int(np.floor(edges.shape[0] / 50.))
all_edge_idx = range(edges.shape[0])
np.random.shuffle(all_edge_idx)
val_edge_idx = all_edge_idx[:num_val]
test_edge_idx = all_edge_idx[num_val:(num_val + num_test)]
test_edges = edges[test_edge_idx]
val_edges = edges[val_edge_idx]
train_edges = np.delete(edges, np.hstack([test_edge_idx, val_edge_idx]), axis=0)
def ismember(a, b):
rows_close = np.all((a - b[:, None]) == 0, axis=-1)
return np.any(rows_close)
test_edges_false = []
while len(test_edges_false) < len(test_edges):
n_rnd = len(test_edges) - len(test_edges_false)
rnd = np.random.randint(0, adj.shape[0], size=2 * n_rnd)
idxs_i = rnd[:n_rnd]
idxs_j = rnd[n_rnd:]
for i in range(n_rnd):
idx_i = idxs_i[i]
idx_j = idxs_j[i]
if idx_i == idx_j:
continue
if ismember([idx_i, idx_j], edges_all):
continue
if test_edges_false:
if ismember([idx_j, idx_i], np.array(test_edges_false)):
continue
if ismember([idx_i, idx_j], np.array(test_edges_false)):
continue
test_edges_false.append([idx_i, idx_j])
val_edges_false = []
while len(val_edges_false) < len(val_edges):
n_rnd = len(val_edges) - len(val_edges_false)
rnd = np.random.randint(0, adj.shape[0], size=2 * n_rnd)
idxs_i = rnd[:n_rnd]
idxs_j = rnd[n_rnd:]
for i in range(n_rnd):
idx_i = idxs_i[i]
idx_j = idxs_j[i]
if idx_i == idx_j:
continue
if ismember([idx_i, idx_j], train_edges):
continue
if ismember([idx_j, idx_i], train_edges):
continue
if ismember([idx_i, idx_j], val_edges):
continue
if ismember([idx_j, idx_i], val_edges):
continue
if val_edges_false:
if ismember([idx_j, idx_i], np.array(val_edges_false)):
continue
if ismember([idx_i, idx_j], np.array(val_edges_false)):
continue
val_edges_false.append([idx_i, idx_j])
# Re-build adj matrix
data = np.ones(train_edges.shape[0])
adj_train = sp.csr_matrix((data, (train_edges[:, 0], train_edges[:, 1])), shape=adj.shape)
adj_train = adj_train + adj_train.T
return adj_train, train_edges, val_edges, val_edges_false, test_edges, test_edges_false
def get_roc_score(edges_pos, edges_neg):
feed_dict.update({placeholders['dropout']: 0})
emb = sess.run(model.embeddings, feed_dict=feed_dict)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Predict on test set of edges
adj_rec = np.dot(emb, emb.T)
preds = []
pos = []
for e in edges_pos:
preds.append(sigmoid(adj_rec[e[0], e[1]]))
pos.append(adj_orig[e[0], e[1]])
preds_neg = []
neg = []
for e in edges_neg:
preds_neg.append(sigmoid(adj_rec[e[0], e[1]]))
neg.append(adj_orig[e[0], e[1]])
preds_all = np.hstack([preds, preds_neg])
labels_all = np.hstack([np.ones(len(preds)), np.zeros(len(preds))])
roc_score = roc_auc_score(labels_all, preds_all)
ap_score = average_precision_score(labels_all, preds_all)
return roc_score, ap_score
Define Convolutional Layers for our GCN Model¶
class GraphConvolution():
"""Basic graph convolution layer for undirected graph without edge labels."""
def __init__(self, input_dim, output_dim, adj, name, dropout=0., act=tf.nn.relu):
self.name = name
self.vars = {}
self.issparse = False
with tf.variable_scope(self.name + '_vars'):
self.vars['weights'] = weight_variable_glorot(input_dim, output_dim, name='weights')
self.dropout = dropout
self.adj = adj
self.act = act
def __call__(self, inputs):
with tf.name_scope(self.name):
x = inputs
x = tf.nn.dropout(x, 1-self.dropout)
x = tf.matmul(x, self.vars['weights'])
x = tf.sparse_tensor_dense_matmul(self.adj, x)
outputs = self.act(x)
return outputs
class GraphConvolutionSparse():
"""Graph convolution layer for sparse inputs."""
def __init__(self, input_dim, output_dim, adj, features_nonzero, name, dropout=0., act=tf.nn.relu):
self.name = name
self.vars = {}
self.issparse = False
with tf.variable_scope(self.name + '_vars'):
self.vars['weights'] = weight_variable_glorot(input_dim, output_dim, name='weights')
self.dropout = dropout
self.adj = adj
self.act = act
self.issparse = True
self.features_nonzero = features_nonzero
def __call__(self, inputs):
with tf.name_scope(self.name):
x = inputs
x = dropout_sparse(x, 1-self.dropout, self.features_nonzero)
x = tf.sparse_tensor_dense_matmul(x, self.vars['weights'])
x = tf.sparse_tensor_dense_matmul(self.adj, x)
outputs = self.act(x)
return outputs
class InnerProductDecoder():
"""Decoder model layer for link prediction."""
def __init__(self, input_dim, name, dropout=0., act=tf.nn.sigmoid):
self.name = name
self.issparse = False
self.dropout = dropout
self.act = act
def __call__(self, inputs):
with tf.name_scope(self.name):
inputs = tf.nn.dropout(inputs, 1-self.dropout)
x = tf.transpose(inputs)
x = tf.matmul(inputs, x)
x = tf.reshape(x, [-1])
outputs = self.act(x)
return outputs
Specify the Architecture of our GCN Model¶
class GCNModel():
def __init__(self, placeholders, num_features, features_nonzero, name):
self.name = name
self.inputs = placeholders['features']
self.input_dim = num_features
self.features_nonzero = features_nonzero
self.adj = placeholders['adj']
self.dropout = placeholders['dropout']
with tf.variable_scope(self.name):
self.build()
def build(self):
self.hidden1 = GraphConvolutionSparse(
name='gcn_sparse_layer',
input_dim=self.input_dim,
output_dim=FLAGS.hidden1,
adj=self.adj,
features_nonzero=self.features_nonzero,
act=tf.nn.relu,
dropout=self.dropout)(self.inputs)
self.embeddings = GraphConvolution(
name='gcn_dense_layer',
input_dim=FLAGS.hidden1,
output_dim=FLAGS.hidden2,
adj=self.adj,
act=lambda x: x,
dropout=self.dropout)(self.hidden1)
self.reconstructions = InnerProductDecoder(
name='gcn_decoder',
input_dim=FLAGS.hidden2,
act=lambda x: x)(self.embeddings)
Specify the GCN Optimizer¶
class Optimizer():
def __init__(self, preds, labels, num_nodes, num_edges):
pos_weight = float(num_nodes**2 - num_edges) / num_edges
norm = num_nodes**2 / float((num_nodes**2 - num_edges) * 2)
preds_sub = preds
labels_sub = labels
self.cost = norm * tf.reduce_mean(
tf.nn.weighted_cross_entropy_with_logits(
logits=preds_sub, targets=labels_sub, pos_weight=pos_weight))
self.optimizer = tf.train.AdamOptimizer(learning_rate=FLAGS.learning_rate) # Adam Optimizer
self.opt_op = self.optimizer.minimize(self.cost)
self.grads_vars = self.optimizer.compute_gradients(self.cost)
Train the GCN Model and Evaluate its Accuracy on a Test Set of Protein-Protein Interactions¶
Given a training set of protein-protein interactions in yeast S. cerevisiae, our goal is to take these interactions and train a GCN model that can predict new protein-protein interactions. That is, we would like to predict new edges in the yeast protein interaction network.
adj = load_data()
num_nodes = adj.shape[0]
num_edges = adj.sum()
# Featureless
features = sparse_to_tuple(sp.identity(num_nodes))
num_features = features[2][1]
features_nonzero = features[1].shape[0]
# Store original adjacency matrix (without diagonal entries) for later
adj_orig = adj - sp.dia_matrix((adj.diagonal()[np.newaxis, :], [0]), shape=adj.shape)
adj_orig.eliminate_zeros()
adj_train, train_edges, val_edges, val_edges_false, test_edges, test_edges_false = mask_test_edges(adj)
adj = adj_train
adj_norm = preprocess_graph(adj)
# Define placeholders
placeholders = {
'features': tf.sparse_placeholder(tf.float32),
'adj': tf.sparse_placeholder(tf.float32),
'adj_orig': tf.sparse_placeholder(tf.float32),
'dropout': tf.placeholder_with_default(0., shape=())
}
# Create model
model = GCNModel(placeholders, num_features, features_nonzero, name='yeast_gcn')
# Create optimizer
with tf.name_scope('optimizer'):
opt = Optimizer(
preds=model.reconstructions,
labels=tf.reshape(tf.sparse_tensor_to_dense(placeholders['adj_orig'], validate_indices=False), [-1]),
num_nodes=num_nodes,
num_edges=num_edges)
# Initialize session
sess = tf.Session()
sess.run(tf.global_variables_initializer())
adj_label = adj_train + sp.eye(adj_train.shape[0])
adj_label = sparse_to_tuple(adj_label)
# Train model
for epoch in range(FLAGS.epochs):
t = time.time()
# Construct feed dictionary
feed_dict = construct_feed_dict(adj_norm, adj_label, features, placeholders)
feed_dict.update({placeholders['dropout']: FLAGS.dropout})
# One update of parameter matrices
_, avg_cost = sess.run([opt.opt_op, opt.cost], feed_dict=feed_dict)
# Performance on validation set
roc_curr, ap_curr = get_roc_score(val_edges, val_edges_false)
print("Epoch:", '%04d' % (epoch + 1),
"train_loss=", "{:.5f}".format(avg_cost),
"val_roc=", "{:.5f}".format(roc_curr),
"val_ap=", "{:.5f}".format(ap_curr),
"time=", "{:.5f}".format(time.time() - t))
print('Optimization Finished!')
roc_score, ap_score = get_roc_score(test_edges, test_edges_false)
print('Test ROC score: {:.5f}'.format(roc_score))
print('Test AP score: {:.5f}'.format(ap_score))